Основные плоские фигуры и их свойства

Основные плоские фигуры включают треугольники, квадраты, прямоугольники, круги и многоугольники. Каждая из этих фигур имеет свои уникальные свойства: треугольники могут быть равносторонними, равнобедренными или разносторонними, что влияет на их углы и стороны, в то время как квадраты и прямоугольники характеризуются прямыми углами и противоположными сторонами, которые равны между собой.

Круг определяется радиусом, а его свойство заключается в том, что все точки на окружности находятся на равном расстоянии от центра. Многоугольники, в свою очередь, имеют количество сторон и углов, которое варьируется, что позволяет им обладать разнообразной формой и свойствами. Таким образом, изучение этих фигур является основой для понимания геометрии и её применения в различных областях.

ТЕМА 19. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ И ИХ СВОЙСТВА

Геометрическая форма — это набор точек.

Отрезок, прямая, круг, шар — все они являются геометрическими фигурами.

Если все точки геометрической фигуры находятся в одной плоскости, то она называется плоской.

Например, отрезок, прямоугольник — это плоские фигуры. Но есть фигуры, которые не плоские, например, куб, шар, пирамида.

Поскольку понятие геометрической фигуры определяется через понятие множества, мы можем говорить о включении одной фигуры в другую, о объединении, пересечении и разности фигур.

Например, если объединить два луча АВ и МК (см. рис. 1), то получится прямая КВ, а их пересечение будет составлять отрезок АМ.

К А М В

Рис. 1

Существуют выпуклые и невыпуклые фигуры.

Фигура является выпуклой, если любые две ее точки содержат соединяющий их отрезок.

Фигура F1, изображенная на рисунке 2, является выпуклой, а фигура F2 — невыпуклая.

Рис. 2

Рис. 3

К выпуклым фигурам относятся плоскость, прямая, луч, отрезок, точка. Можно убедиться в том, что круг является выпуклой фигурой (рис. 3). Если продолжить отрезок XY до пересечения с окружностью, то получим хорду АВ. Поскольку хорда содержится в круге, то и отрезок XY содержится в круге, а значит, круг — выпуклая фигура.

У многоугольников существует другое определение: многоугольник является выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону.

Поскольку равнозначность этого определения и вышеприведенного определения для многоугольника доказана, то можно использовать и то, и другое.

Исходя из этих понятий, рассмотрим другие геометрические фигуры, изучаемые в школьном курсе планиметрии. Рассмотрим их определения и основные свойства, принимая их без доказательства. Знание этого материала и умение применять к решению простых геометрических задач является базой для разработки методики обучения младших школьников основам геометрии.

Углы

Напомним, что угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Лучи называются сторонами угла, а их общее начало — его вершиной.

Угол обозначают по-разному: указывают либо его вершину, либо его стороны, либо три точки: вершину и две точки на сторонах угла: #xD0(k,l), количество просмотров: 508 ;

Что это такое?

Основы геометрии лежат в основе геометрических фигур. Это кажется логичным, не так ли? Однако их множество, и нужно знать абсолютно все, потому что они могут быть описаны условием без чертежа, и тебе придется угадывать, что просят найти составители. Давай разберемся с основными геометрическими фигурами планиметрии, чтобы у тебя хотя бы не было проблем с простой проверкой фактов.

Итак, структура будет простой — сначала изображение, затем информация, и опять все сначала. Все понятно? Тогда начинаем!

Вероятно, у тебя нет проблем с определением квадрата, не так ли? Это та фигура, с которой мы сталкиваемся еще с детства — играем, изучаем, взаимодействуем. Давай быстро подытожим основные свойства: все стороны равны — главное правило! Противоположные стороны параллельны, сумма углов равна 360 градусам — это относится ко всем параллелограммам.

Ты, вероятно, обратишь внимание на еще один факт, который может пригодиться для быстрого решения тестовых задач — диагонали квадрата равны по длине, пересекаются под прямым углом и делят друг друга пополам. Это важно для тех, кто готовится к экзаменам, таким как ЕГЭ или ОГЭ, в которых проверяются базовые знания геометрии.

Прямоугольник

Еще одна известная геометрическая фигура — это прямоугольник. Основные характеристики: противоположные стороны равны и параллельны. Это опять же следует из свойств параллелограмма — в конце концов, эта фигура и предыдущая являются его частными случаями, поэтому существует много общих черт. Опять же у нас получится сумма углов в 360 — для всех замкнутых фигур с четырьмя вершинами такое свойство. Диагонали опять равны и пересекаются в точке, делающей их пополам.

Трапеция

Мы подошли к менее известным геометрическим фигурам, если ты только начинаешь изучать геометрию. Один из ключевых моментов – сумма углов, прилегающих к боковой диагонали, равна 180 градусам. Это знание будет полезным во многих задачах по трапеции.

Ромб

Фигура "ромб" встречается не так часто в математических задачах, но все равно важно знать его особенности. Основное правило — все четыре высоты равны друг другу.

Как обычно, изображение сверху, чтобы увидеть, как выглядит рисунок. Один из ключевых аспектов этой темы — разница между кругом и окружностью. Чем они отличаются? Давайте посмотрим: окружность — это замкнутая кривая, где все точки равноудалены от центра. А круг — это геометрическая фигура, ограниченная окружностью.

Именно поэтому важно знать их различия, чтобы не путать их между собой.

Треугольник

Очень любимый друг всех задач и решений. Многие задачи можно решить, даже если ты знаешь только о треугольнике — такой он хороший. Особенно рекомендуем изучить прямоугольный треугольник — он встречается так часто, что даже страшно становится.

Параллелограмм

Фигуры, такие как квадрат, ромб и параллелограмм, являются частными случаями особого геометрического образования. Именно поэтому важно знать не только о их существовании, но и об их особенностях и характеристиках. Если тебе трудно запомнить все эти свойства, то напиши их на бумаге и время от времени повторяй, чтобы не забыть.

Точка

Прямая

Отрезок

Луч

Угол

Эти пять форм — начальные концепции, которые ученики исследуют в начальной школе. Из них вырабатываются другие формы и идеи, поэтому важно запомнить их названия и различия.

Основные величины

Что такое площадь? Это часть плоскости, заключенная внутри фигуры, например в треугольнике. Этот термин встречается довольно часто в учебниках и задачах, поэтому важно понимать его значение. Как ее найти? Просто перемножьте длину на ширину — и вы узнаете, сколько территории находится внутри.

Периметр — это сумма всех сторон.

Найти его довольно просто и логично, но некоторые формулы для фигур делают работу еще проще. Например, для квадрата не нужно записывать сумму отдельно, вы можете просто узнать, какая длина одной стороны и умножить ее на 4. Та же схема работает и для параллелограмма — умножайте боковую сторону на основание в два раза, и смысл "упрощения" остается таким же.

Владислав Смирнов

Результаты выпускников Турбо на ЕГЭ по профилю:

Более 40 учеников получили 100 баллов на экзамене
187 человек набрали 90+ баллов на ЕГЭ, 1703 ученика сдали экзамен на 80+ баллов
Ученики годового курса улучшили свой результат на 53 балла
Средний результат наших учеников на 13 баллов выше среднего по России
Нашим выпускникам удается поступить в такие университеты, как МГУ, ВШЭ, МГИМО, СПбГУ, РАНХиГС, КФУ, РЭУ Плеханова и другие топовые вузы."

Обо мне:

Я окончил физико-математический лицей, затем поступил на экономический факультет Санкт-Петербургского государственного экономического университета.
Я возглавлял Молодежный Экономический Клуб в СПбГЭУ, основал всероссийскую Молодежную Ассоциацию Клубов Управленческой Борьбы, и проводил занятия в десятках вузов различных городов.
Я регулярно сдаю ЕГЭ, последний раз мой балл был 94.
Для эффективной подготовки я лично поддерживаю контакт с каждым учеником, создавая уютную атмосферу на вебинарах!
Для лучшего усвоения материала на вебинарах мы устраиваем перекуры, выпиваем коктейль из колы и молока, а также заказываем пиццу.

До встречи на вебинарах! ❤️

Виды треугольников по сторонам

A C B E D F Равносторонний треугольник Равнобедренный треугольник Разносторонний треугольник Начало

• Медианы треугольника • Высоты треугольника • Проверочные задания • Биссектрисы треугольника Начало

Треугольники

• Основные свойства равенства треугольников • Основные признаки равенства прямоугольных треугольников • Основные критерии подобия треугольников • Методы решения задач Начало

Треугольник, у которого один из углов равен 90 градусов, называется прямоугольным. Каждый такой треугольник имеет прямой угол.

Свойства геометрических фигур на плоскости

У каждой геометрической фигуры есть свои уникальные свойства, которые делают её узнаваемой и полезной в различных задачах.

Сумма всех внутренних углов равна 180°
Сумма двух сторон должна быть больше третьей стороны
Медианы, проведенные из вершин треугольника, пересекаются в одной точке

Свойства четырехугольника

Сумма всех углов в четырехугольнике равна 360°
В случае выпуклых четырехугольников их диагонали пересекаются в центре

Понимание этих свойств позволяет быстро вычислять различные параметры геометрических фигур, необходимые для решения множества практических задач.

Помните!

Окружность представляет собой геометрическую фигуру, образованную замкнутой кривой линией, все точки которой находятся на одинаковом расстоянии от центра.

Круг — это геометрическая фигура, ограниченная окружностью.

Окружность — это граница круга.

Радиус круга — это расстояние от центра окружности до любой ее точки.

Диаметр круга — это отрезок, соединяющий две точки окружности и проходящий через ее центр.

Диаметр круга равен двум его радиусам.

O — середина окружности.
AB — диаметр окружности (обозначается буквой « d »).
OK — радиус окружности (обозначается буквой « r »).
АB = 2OK

Ваши комментарии

Необходимо помнить об этом!

Для возможности оставить свой отзыв, необходимо авторизоваться через социальную сеть "ВКонтакте".

2 ноября 2020 в 15:06

Elena Khz Профиль Благодарили: 0 Сообщений: 2

В треугольнике одна сторона больше другой на 2 см и больше третьей на x см. Какова длина третьей стороны, если вторая сторона равна 10 см? Найдите значение этого выражения при x=1 и x=у

2 ноября 2020 в 17: для Elena Khz

Elena Khz Профиль Благодарили: 0 Сообщений: 2

При x=1 и x=3

7 января 2017 в 11:21

Елена Белякова Профиль Благодарили: 0 Сообщений: 1

нарисуйте прямоугольник, у которого периметр равен 20см, а площадь -24см

11 февраля 2017 в 15: для Елена Белякова

Алексей Карапов Профиль Благодарили: 0 Сообщений: 9

Предположим, что А-длина; Б-ширина; Р-периметр; С-площадь; Р=(А+Б) · 2; С=А · Б; Необходимо найти два числа, умножение которых даст нам площадь равную 24 см, а их сложение и умножение на два — периметр 20 см. Существует много вариантов, и я приведу лишь один из них: вариант А-6 см; Б-4 см; Р-(4+6) · 2=10 · 2=20 см; С-4 · 6=24 см; Возможно поменять местами А и Б, и результат не изменится в соответствии с правилом "если множители поменять местами, то произведение не изменится".

8 июня 2016 в 13:11

Дарья Бондарь Профиль Благодарили: 0 Сообщений: 4

Как сравнить два отрезка?9 июня 2016 в 10: для Дарья Бондарь

Евгений Колосов Профиль Благодарили: 12 Сообщений: 197

Можно визуально сравнить, оценив их длину. Можно измерить отрезки линейкой и сравнить значения. Можно поместить начала отрезков в одну точку и разместить их на одной прямой, чтобы увидеть разницу.

8 июня 2016 в 9:22

Дарья Бондарь Профиль Благодарили: 0 Сообщений: 4

Узнайте, какие фигуры называются равными?

8 июня 2016 в 12: для Дарьи Бондарь

Евгений Фёдоров Профиль Благодарили: 0 Сообщений: 60

Узнайте, какие из них переходят друг в друга при перемещении.

14 августа 2015 в 12:38

Михаил Городовой Профиль Благодарили: 0 Сообщений: 3

Секция "Начальная школа" посвящена изучению фигур и их свойств. Здесь мы находим следующие определения: 1. Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой расположены на одинаковом расстоянии от центра. 2. Круг — это геометрическая фигура, ограниченная окружностью. 3. Окружность — это граница круга.

4. Радиус круга — это расстояние от центра окружности до любой её точки. Однако, по моему мнению, 4-ое определение неверно, поскольку у самой окружности нет центра. В данном случае 4-ое определение лишено смысла. Лучше сформулировать его так: — Радиус круга — это расстояние от центра круга до любой точки на окружности.

14 августа 2015 в 15: для Михаил Городовой

Борис Гуров Профиль Благодарили: 4 Сообщений: 32

Время и дата: 16 августа 2015, 12:53

Пользователь: Михаил Городовой

Статистика: Профиль Благодарили: 0 Сообщений: 3

Определения, представленные в моей теме на этом сайте, указывают на различие между окружностью и кругом как двумя разными геометрическими фигурами. Согласно этим определениям, радиус круга — это расстояние от центра круга до любой точки на его окружности, а не от центра окружности до любой точки на ней.

Равносторонние треугольники

Фигура, у которой все стороны одинаковые, называется равносторонней. Это равносторонний треугольник.

Фигура, у которой все стороны разной длины, называется разносторонней. Это разносторонний треугольник.

Медиана треугольника

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Длина DE = 4.11 см. Любой треугольник имеет три медианы. В треугольнике медианы пересекаются в одной точке.

Высота — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Любой треугольник имеет три высоты. В треугольнике высоты пересекаются в одной точке. О T Q P QT

Геометрические фигуры на плоскости

Если все тонкие фигуры принадлежат одной плоскости, то геометрическая фигура считается плоской.

Прямая, отрезок, круг, различные многоугольники и другие подобные фигуры являются примерами плоских геометрических фигур. В то время как шар, куб, цилиндр, пирамида и подобные им не являются плоскими.

В плоскости можно выделить два типа фигур: выпуклые и невыпуклые.

Фигура считается выпуклой, если она содержит отрезок, концами которого являются любые две точки, принадлежащие фигуре (рис. 54).

Примерами выпуклых фигур являются: круг, различные треугольники, квадрат, а также точка, прямая, луч, отрезок и плоскость.

Важнейшие понятия геометрии на плоскости — точка и прямая. Эти понятия активно используются даже при работе с самыми маленькими детьми. Необходимо научить детей узнавать эти фигуры, изображать их, понимать и правильно выполнять задания вовремя.

Основные свойства точек и прямых определены аксиомами:

1. На прямой существуют как точки, так и точки, не принадлежащие ей.

2. Через две различные точки можно провести только одну прямую.

3. Две различные прямые либо не пересекаются вовсе, либо пересекаются в одной точке.

Дети, например, играя или рисуя, знакомят с собой точку, отрезок, различные линии, выделяя из них прямую, кривую, ломаную, учатся распознавать некоторые из их свойств.

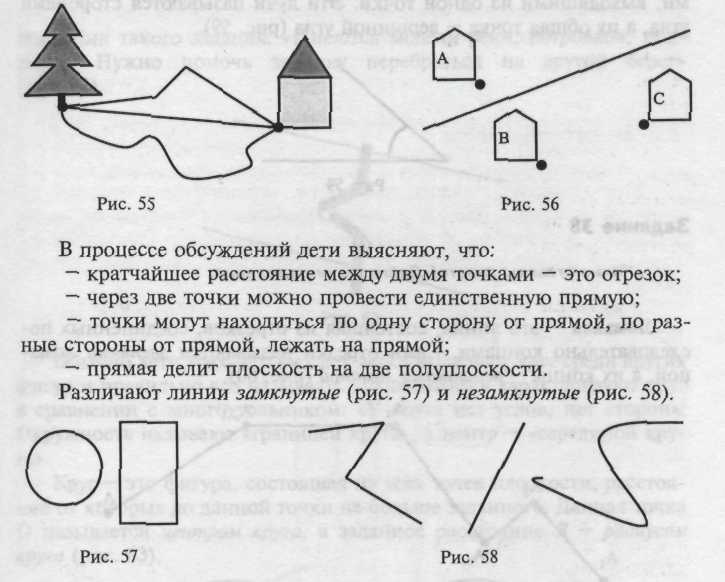
1. "Какая дорога от леса до дома короче?" (рисунок 55).

2. "Маленькие свинки обитают в уютных домиках, стоящих у воды. Они не способны плавать. Какое из поросят может сходить в гости к своим соседям?" (см. картинку 56).

Разделенная замкнутая линия разделяет плоскость на внешнюю и внутреннюю области, что дети понимают рано. Например, при выполнении заданий на закрашивание фигур – внутренняя область.

Геометрические фигуры, с которыми знакомятся дети (круг, квадрат, треугольник и другие), представляют собой замкнутые линии (границы фигур) с их внутренней областью. Границей круга является окружность. Границей многоугольников является ломаная линия, состоящая из отрезков. В геометрии для всех этих понятий существуют определения.

Отрезок – это часть прямой, состоящая из всех точек этой прямой, лежащих между двумя данными точками, называемыми концами отрезка.

Луч (полупрямая) – это часть прямой, состоящая из всех ее точек, лежащих по одну сторону от заданной на ней точки (начала луча).

Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки. Такие лучи называются сторонами угла, а их общая точка — вершина угла (см. рисунок 59).

Фигурой, состоящей из окружности и ее внутренней области, можно определить круг.

Окружность представляет собой множество точек плоскости, равноудаленных от заданной точки. Центр окружности называется О, а его радиус обозначается R (рис. 64).

В детском саду дети также знакомятся с овалом («фигурой, похожей на круг тем, что у нее нет углов и сторон, но отличающейся от круга своей вытянутостью»). В геометрии такой термин не рассматривается, но изучается эллипс. Его нецелесообразно предлагать детям из-за сложности построения. Однако в быту часто используются слова «овал», «предмет овальной формы», поэтому знания об овале необходимы детям как элемент сенсорного воспитания и развития речи.

Многоугольники

Многоугольник — это часть плоскости, ограниченная простым замкнутым ломаным линиями. Стороны многоугольника называются звеньями ломаной, а вершины — вершинами фигуры. Граница многоугольника (простая замкнутая ломаная) также называется многоугольником.

При работе с дошкольниками обычно используются модели фигур из картона, пластмассы или дерева, а также проводятся задания по рисованию многоугольников с помощью трафаретов и обводок, а также раскрашиванию фигур. В ходе этих занятий дети учатся называть фигуры, изучают их структуру и некоторые свойства, используя такие термины, как: граница фигуры, внутренняя область фигуры и другие.

Выпуклый многоугольник лежит в одной полуплоскости относительно любой прямой, содержащей его сторону (рис. 65).

Нравится статья? Добавь ее в закладки (CTRL+D) и не забудь поделиться с друзьями:

Основные плоские фигуры и их свойства

webkonspect.com — ресурс, который сочетает в себе возможности социальной сети и предназначен для помощи студентам в их учебной деятельности.

Здесь вы сможете составить свой конспект, который окажет вам поддержку в процессе обучения.

Что делает webkonspect.com полезным:

Простота создания и редактирования конспекта (200 вопросов в 3 клика).
Просмотр конспекта без подключения к интернету.
Удобный текстовый редактор, который позволяет вам форматировать текст, создавать таблицы, вставлять математические формулы и фотографии.
Возможность совместного создания конспекта с другом или одногрупником.
webkonspect.com — надежное хранилище небольших файлов.

Обзор сайта: