Перемещение в физике определяется как векторная величина, которая показывает изменение положения тела в пространстве. Оно учитывает начальную и конечную точки, а также направление движения, что отличает его от пройденного пути, который является скалярной величиной и не включает в себя направление.
Для расчета перемещения можно использовать формулу, которая связывает начальные и конечные координаты: S = Sконечное — Sначальное. Таким образом, перемещение может быть как положительным, так и отрицательным, в зависимости от направления движения относительно заданной системы координат.
Конспект урока Тема: «Перемещение при прямолинейном равноускоренном движении». план-конспект урока по физике (9 класс) на тему
Содержание урока: Тема занятия — "Перемещение при прямолинейном равноускоренном движении".
Изучаемый материал: учебник Перышкин. А.В. 9 класс.
Тип занятия: урок изучения нового материала.
Стратегические цели: формирование научного мировоззрения учащихся, знакомство с понятием прямолинейного равноускоренного движения.
Тактические цели: развитие умения мобилизоваться и применять имеющиеся знания при самостоятельном решении задач; развитие логического мышления; формулирование четких и лаконичных ответов на вопросы; анализ и синтез; выделение главного и делание выводов; определение существенных признаков объектов.
Необходимо повторить, суммировать и закрепить умения основных понятий, терминов и формул по вопросу прямолинейного равноускоренного движения. Также нужно ознакомить учащихся с выводом формулы проекции вектора перемещения для данного вида движения.
Студенты будут работать как в целом, так и индивидуально.
Для этого потребуются компьютер, мультимедийный проектор, доска, учебник и журнал.
Методы обучения будут включать в себя словесный, практический и объяснительно-иллюстративный.
Слово учителя, журнал
Изучение нового материала
Методический подход — словесный. Показательный
Закрепление новой учебной информации (решение задач)
Метод применения — практический, словесный
Сводка занятия
Приветствие студентов и знакомство с ними, запись отсутствующих студентов в классном журнале, объявление темы урока, запись на доске и в тетрадях студентов
- Актуализация знаний
Перед продолжением изучения темы, давайте вспомним и повторим изученное ранее.
- Как называется равномерное, прямолинейное движение?
- Что такое скорость равномерного движения?
- В каких единицах измеряется скорость?
- Как перевести скорость из км/ч в м/с.
- В каких случаях проекция скорости равномерного движения на ось положительна, а в каких отрицательна?
Послушав ответы учеников, я предлагаю им выполнить небольшую самостоятельную работу на карточках.
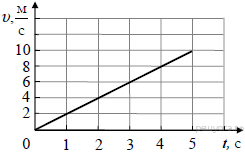
- Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 5-ой секунды, при условии, что характер движения тела не изменяется
- 9 м/с
- м/с
- м/с
- м/с
- За 30 секунд поезд двигался равномерно со скоростью 54 км/ч. Какой путь он прошел за это время?
- По графику скорости, изображенному на рисунке, определите путь, пройденный телом за 5 секунд.
- При равномерном движении пешеход проходит путь 12 метров за 6 секунд. Какой путь он пройдет при движении с той же скоростью за 3 секунды?
- Изучение нового материала
Для того чтобы рассчитать проекцию вектора перемещения тела, движущегося прямолинейно и равноускоренно, за любой промежуток времени, необходимо использовать определенную формулу. Эту формулу мы можем найти на рисунке 14 на стр. 29 учебника, где отрезок AC представляет график проекции вектора скорости тела, движущегося с постоянным ускорением a.
Итак, вопрос к классу: по какой формуле при прямолинейном равномерном движении тела определяется вектор перемещения? Ответ: по той же формуле, что и площадь прямоугольника, заключенного под графиком проекции вектора скорости.
Таким образом, мы можем сделать вывод, что проекция вектора перемещения численно равна площади этого прямоугольника.
Докажем, что при прямолинейном равноускоренном движении проекцию вектора перемещения можно определить с использованием той же формулы, что и площадь фигуры, ограниченной графиком АС, осью Оt и отрезками ОА и ВС. Иначе говоря, в этом случае проекция вектора перемещения численно равна площади фигуры под графиком скорости. Для этого на оси Оt (рис. 14а) выделим небольшой промежуток времени db. Из точек d и b проведем перпендикуляры к оси Оt до их пересечения с графиком проекции вектора скорости в точках a и c.
Таким образом, за промежуток времени, соответствующий отрезку db, скорость тела меняется от .
За достаточно малый промежуток времени проекция вектора скорости меняется очень незначительно, поэтому движение тела в течение этого промежутка времени мало отличается от равномерного, т.е. от движения с постоянной скоростью.
Если участок AC графика считать горизонтальной, а полоску ACBD — прямоугольником, то площадь этой полоски будет равна проекции вектора перемещения за промежуток времени, соответствующий отрезку DB.
Вся площадь фигуры OACB можно разделить на такие полоски. Какой же фигурой является фигура OACB?
Следовательно, какова проекция вектора перемещения за промежуток времени, соответствующий отрезку OV? (площадь трапеции определяется по той же формуле).
Какова площадь трапеции?
Из рисунка 14б найдем основания и высоты трапеции. Назовите их.
Таким образом, с учетом вышесказанного, выведем формулу для вычисления площади трапеции. Итак:
Напомним, какова скорость при равномерном равноускоренном движении?
Учитывая, что S=S x , формулу (1) можно записать по-другому. Каждый ученик записывает эту формулу в свою тетрадь и проверяет ее с тем, что учитель пишет на доске.
Таким образом, мы получаем формулу для расчета проекции вектора перемещения при равноускоренном движении.
По этой же формуле можно рассчитать проекцию вектора перемещения при движении тела с уменьшающейся скоростью, но в этом случае векторы скорости будут направлены в противоположные стороны, и их проекции будут иметь разные знаки.
Просмотр видеофрагмента «Демонстрация равноускоренного прямолинейного движения». Задание для учащихся после просмотра.
- Закрепление учебного материала.
Путь. Перемещение. Проекция вектора на ось. Определение координаты движущегося тела | Конспект
Перемещение представляет собой вектор, который соединяет начальное положение тела с его последующим положением.
(overrightarrow) – вектор перемещения
S – модуль вектора (overrightarrow) (длина)
(S_) – проекция вектора (overrightarrow) на ось Х
Движение является криволинейным, когда тело движется по кривой (ломаной); прямолинейным – когда тело движется по прямой.
Траектория – это линия, по которой движется тело.
Путь – это длина траектории.
Прямолинейное равномерное движение – это когда тело проходит равные пути за равные промежутки времени. В этом случае скорость тела остается постоянной векторной величиной. v = const
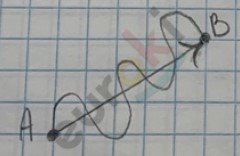
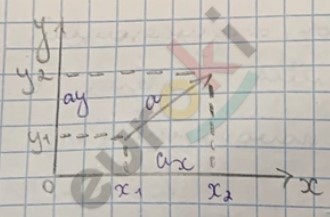
Перемещение это расстояние между начальным и конечным положением объекта в пространстве.

Вектор представляет собой отрезок, имеющий определенное направление.

ax – это отображение вектора на ось x
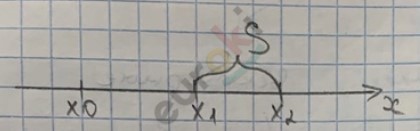
Уравнение движения представляет собой x = x0 + Sx
где x0 — начальная координата
а x — конечная координата
и Sx — проекция перемещения
Подробнее можно узнать в разделе ⏱ Физика > Путь. Перемещение. Проекция вектора на ось. Определение координаты движущегося тела
Пересказ параграфа по физике 9 класс тема перемещение
1. Что значит проходить путь?
Траектория представляет собой воображаемую линию, по которой движется объект. Пройденный путь — это длина траектории. Путь — это скалярная величина, не имеющая направления. Обозначение пройденного пути — s. Единица измерения пути в системе СИ — 1 метр.
2. Можно ли всегда определить положение объекта в заданный момент времени t, зная его начальное положение (при t0 = 0) и пройденный путь за промежуток времени t?

От начальной точки тело может двигаться в разных направлениях, проходя одинаковые пути. Траектория движения тела не всегда совпадает с его перемещением. Поэтому нельзя однозначно определить положение тела, зная начальное положение и путь, пройденный за промежуток времени t.
3. Что представляет собой перемещение тела (материальной точки)?
Перемещение тела (материальной точки) — это вектор, соединяющий начальное положение тела с его последующим положением.

Перемещение это вектор, который обозначается буквой s, также как и путь. Его модуль измеряется в метрах, с единицей измерения в 1 метре. Для измерения используются также другие единицы длины: километры, мили.
4. Можно ли однозначно определить положение тела в определенный момент времени t, если известно его начальное положение и вектор перемещения за промежуток времени t?
Если известно начальное положение и вектор перемещения тела, то можно однозначно определить его местоположение.
5. Почему в механике важнее вектор перемещения, чем пройденный путь?
Вектор перемещения однозначно определяет положение тела при перемещении.
Вернуться к "Оглавлению" — смотреть
Сложение путей
Давайте рассмотрим, как мы можем вычислить общий путь, состоящий из нескольких отрезков.
Например, самолет летит на север на расстояние $100 space км$. Затем поворачивает на запад и пролетает $150 space км$, и затем летит еще $300 space км$ на юго-запад (см. рисунок 4).
Путь представляет собой скалярную величину. Поэтому мы будем складывать пути арифметически: $s = s_1 + s_2 + s_3 = 100 space км + 150 space км + 300 space км = 550 space км$.
Вычитание и сложение перемещений
При выполнении подобных операций с перемещениями необходимо придерживаться правил сложения и вычитания векторов.
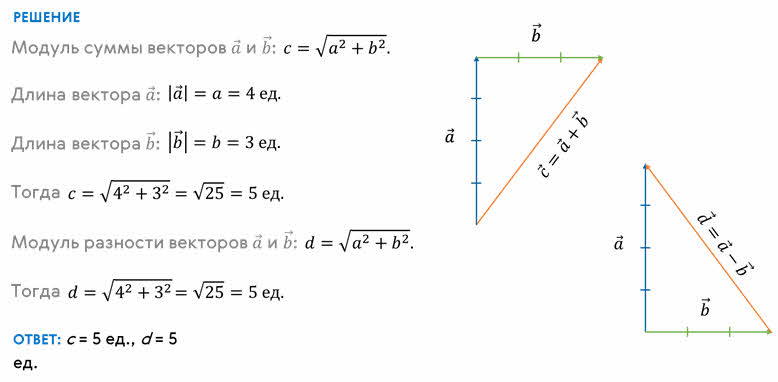
В случае, если два вектора $vec a$ и $vec b$ имеют одинаковое направление, то их сумма представляет собой вектор $vec c$ того же направления. Его длина будет равна сумме длин данных векторов: $ vec c = vec a + vec b $ (см. рисунок 5).
Если направления векторов $vec a$ и $vec b$ противоположны, то их сумма также является вектором $vec c$ с одинаковым направлением с вектором, модуль которого больше ($vec a$). Длина конечного вектора будет равна разности длин слагаемых векторов: $ vec c = vec a − vec b $ (см. рисунок 6).
Правило параллелограмма
Если векторы расположены под углом друг к другу, то можно использовать правило параллелограмма.
Для этого нужно соединить начала векторов $vec{a}$ и $vec{b}$, сложить их, и построить параллелограмм на основе этой суммы (см. рисунок 7).
Суммой этих векторов будет вектор $vec{c}$, начинающийся в точке, где находятся начальные точки векторов $vec{a}$ и $vec{b}$, и направленный по большей диагонали параллелограмма.
Правило треугольника
При работе с векторами также полезно применять правило треугольника. Для этого необходимо соединить конец одного вектора с началом другого (см. рисунок 8). Таким образом, мы получаем вектор $vec c$, который представляет собой сумму векторов $vec a$ и $vec b$.
Правило многоугольника
Если мы захотим сложить несколько векторов, то прибегаем к правилу многоугольника.
Например, у нас есть четыре вектора $vec a$, $vec b$, $vec c$ и $vec d$. Для сложения их мы располагаем векторы так, чтобы каждый следующий начинался от конца предыдущего (см. рисунок 9). Затем проводим линию от начала первого вектора $vec a$ до конца последнего $vec d$ и получаем суммарный вектор $vec e.
Вычитание векторов
В случае необходимости вычислить разность двух векторов $vec a$ и $vec b$, необходимо соединить их начала. Затем проводится вектор $vec c$ ($vec c = vec a — vec b$) от конца вектора $vec b$ к концу вектора $vec a$ (см. рисунок 10).
Физика 9 класс. Урок№2. Перемещение
При передвижении тела его положение в пространстве изменяется со временем. До настоящего момента для решения большинства задач по движению тел мы использовали понятие "путь", оно вам, наверное, хорошо известно. Напомним, что путь — это длина траектории, пройденной телом за определенное время.
А траектория — это воображаемая линия в пространстве, по которой тело движется.
Путь чаще всего обозначают малой латинской буквой s, и в СИ его единицей является метр.
Путь — это скалярная величина, то есть величина, имеющая числовое значение, но не имеющая направления.

Если траектория движения тела известна, и известно его начальное положение на этой траектории, и пройденное за некоторое время расстояние, то через некоторое время можно определить его положение. Но если траектория движения тела неизвестна, то его положение в конкретный момент времени определить невозможно, потому что он мог пройти одно и то же расстояние в разных направлениях. Давайте рассмотрим это на примере.
Предположим, что лыжник вышел из лыжной базы, находящейся 20 километров к северу от города, и пройдя 20 километров за 2,5 часа. Как определить, где он находится? Ведь он мог быть в разных местах, находящихся не дальше чем в 20 километрах от лыжной базы. Он мог дойти до города, но также мог пройти 10 километров в каком-то другом направлении и вернуться на базу.
При этом его путь будет составлять 20 километров, но его положение в пространстве будет разным в каждом конкретном случае.
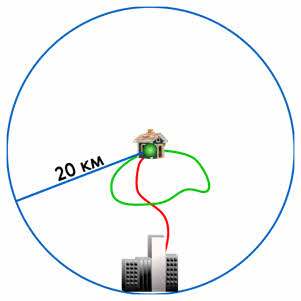
Для определения местоположения лыжника необходимо знать направление его движения и расстояние, которое он прошел в этом направлении. Путь, соединяющий начальное положение тела с его конечным положением, называется перемещением тела.
Таким образом, перемещение представляет собой векторную величину, имеющую направление и численное значение (модуль).
Перемещение обозначается маленькой латинской буквой s с стрелочкой над ней, так же как и путь. Единицей измерения перемещения в СИ является метр.
Таким образом, если мы знаем начальное положение тела и его перемещение за определенный период времени, мы можем легко определить его положение в конце этого периода времени.
— Как складываются и вычитаются пути и перемещения?
Так как путь — это скалярная величина, то можно складывать и вычитать пройденные пути арифметически. Например, если известно, что катер проплыл 10 километров на север, затем 15 километров на восток и ещё 30 километров на юго-восток, то общий пройденный катером путь равен 55 километрам.
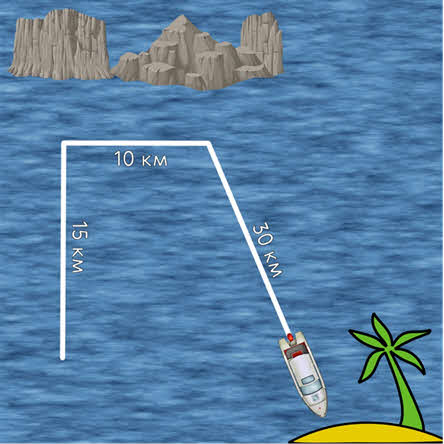
Операции перемещения выполняются в соответствии с правилами сложения и вычитания векторов.
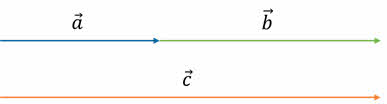
Давайте вспомним, как происходит сложение векторов. Если два вектора направлены в одном направлении, то их сумма — это вектор с таким же направлением, чей модуль равен сумме модулей этих двух векторов.
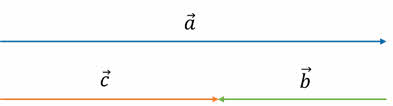
В случае, если направления векторов противоположны, то их сумма является вектором, направленным в том же направлении, что и вектор с большим модулем. При этом модуль полученного вектора равен разности модулей слагаемых векторов.
— Как можно сложить векторы, направленные под разными углами?
На это есть несколько способов. Один из них называется правилом параллелограмма.
Для сложения двух векторов с помощью этого правила, нужно сдвинуть начало одного из векторов так, чтобы оно совпало с концом другого вектора. Затем нужно построить параллелограмм, в котором сторонами будут являться слагаемые векторы. Сумма векторов будет представлять собой вектор, совпадающий с большей диагональю параллелограмма.
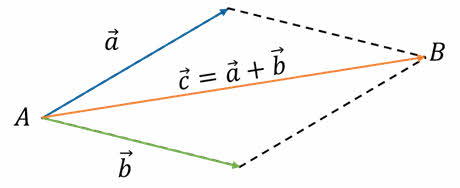
Правило треугольника — второе правило для сложения векторов. Согласно данному правилу, для получения суммы двух векторов необходимо параллельным переносом совместить конец одного вектора с началом второго. В результате получится вектор, соединяющий начало первого вектора с концом второго, который будет равен их сумме.
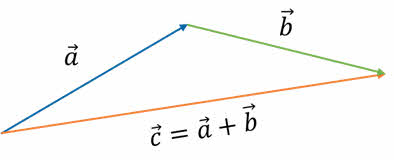
Если необходимо вычислить сумму нескольких векторов, то нужно переместить их параллельно так, чтобы каждый последующий вектор начинался там, где заканчивается предыдущий. Вектор, соединяющий начало первого вектора с концом последнего, будет представлять собой сумму всех данных векторов. Этот метод сложения известен как правило многоугольника.
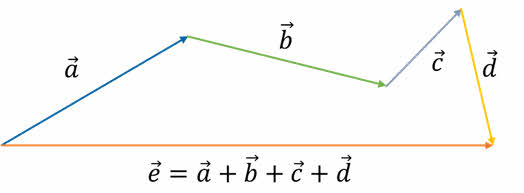
Итак, если необходимо вычислить разность двух векторов, то сначала нужно совместить начала векторов a и b при помощи параллельного переноса. Затем нужно провести вектор от конца вычитаемого вектора к концу вычитаемого вектора.
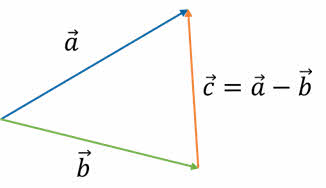
Если вспомнить правила сложения и вычитания векторов, можно с уверенностью утверждать, что в общем случае перемещение не совпадает с траекторией движения тела. А модуль перемещения соответствует пройденному пути.
Например, представим, что автомобиль отправился из Москвы в Санкт-Петербург и вернулся обратно. Самый короткий автомобильный маршрут от центра Москвы до центра Санкт-Петербурга равен 710 километрам. Таким образом, путь, который преодолел автомобиль, составляет 1420 километров. Однако его перемещение равно нулю.
Поэтому запомните, что модуль перемещения и пройденный путь равны только в том случае, если тело движется по прямой траектории в одном направлении. Другими словами, путь не может быть короче модуля перемещения.
Закрепление материала.
Рассчитайте сумму и разность взаимно перпендикулярных векторов a и b. Определите модули суммы и разности этих векторов.
В конце занятия предлагаю рассмотреть, зависит ли форма траектории, путь и перемещение от выбора системы отсчета. Для этого проведем такой эксперимент. Прикрепим к диску вертикальную рейку в его центре и раскрутим диск. Теперь проведем вдоль рейки мелом от центра диска вниз. При таком движении в системе отсчета, связанной с Землей, траекторией мела является прямая линия.
При этом путь и модуль перемещения мела будут одинаковы.
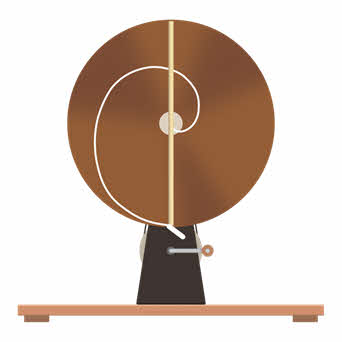
Но когда на диске происходит этот процесс, на нем появляется спираль, которая отображает путь, по которому двигается тот же мел в системе координат, связанной с диском, и этот путь является изогнутым.
Еще один эксперимент описан в книге Галилея "Диалог о двух системах мира". Суть эксперимента заключается в следующем: с вершины мачты плывущего корабля на его палубу падает ядро. В системе координат, связанной с кораблем, траектория движения ядра — это прямая линия.
Однако с точки зрения наблюдателя, стоящего на берегу, ядро имело определенную начальную горизонтальную скорость, равную скорости корабля. Поэтому траектория движения ядра изогнута.

Таким способом, на данном примере мы можем увидеть, что форма траектории, путь и передвижение объекта в различных системах отсчета отличаются.
Практическое задание
страница 10 — 12
упражнение №2

Путешествие по Турции
На этой странице вы узнаете об удивительной культуре, богатой истории, уникальных традициях и обычаях этой прекрасной страны.
Урок физики в 9 классе "Перемещение. Путь"


Учебный материал по физике для 9 класса "Перемещение. Путь" полностью соответствует требованиям современного урока, составленного согласно стандартам второго поколения ФГОС. Цель урока — усвоение новой физической величины — ускорения. Программа урока включает все основные этапы. Урок физики для 9 класса "Перемещение. Путь"
ур2 путь. перемещение.pptТраектория представляет собой линию, по которой движется тело. Путь — это длина траектории, которую тело преодолело за определенный период времени. Перемещение тела — это вектор, соединяющий начальное и конечное положения тела
Определение пройденного пути и перемещения. Вывод: перемещение тела всегда меньше пройденного пути.
Возможно ли, что перемещение объекта равно 0? Ограничивается ли это только движением по кругу? Может ли перемещение быть равно расстоянию? Итак, вывод таков: перемещение может быть равным пройденному пути, меньше этого значения или даже равно 0.
Кинематика. Перемещение и путь
Перемещение в терминах механики означает направленный вектор (отрезок прямой линии), который соединяет начальное и конечное положения тела.
Понятие вектора перемещения вводится с целью решения задач кинематики — определить местоположение тела в пространстве в определенный момент времени, если известно его начальное положение.
Предположим, что точка М движется по изогнутой траектории и в определенные моменты времени t1 и t2 находится в точках М1 и М2 соответственно. Вектор перемещения соединяет эти два положения и представляет собой вектор перемещения. Если положение точки М1 задается радиус-вектором , а точки М2 – радиус-вектором , то вектор перемещения будет равен разности этих двух векторов:
Путь — это длина участка траектории, пройденного объектом за определенное время. В общем случае модуль вектора перемещения не равен длине пути, пройденного объектом за определенное время, потому что траектория может быть изогнутой, и объект может изменять направление движения.
Модуль вектора перемещения и путь могут совпадать только при прямом движении в одном направлении. При изменении направления прямолинейного движения, модуль вектора перемещения будет меньше пути.
При изогнутом движении модуль вектора перемещения также будет меньше пути, потому что хорда всегда меньше дуги, которую она описывает.
Конспект урока на тему "Перемещение при прямолинейном равноускоренном движении", 9 класс
Перестановка №7 в рамках прямолинейного равноускоренного движения в 9 классе пособия Перышкина.
Вы уже знакомы с суперспособностями современного учителя?
![]()
Максимально экономить энергию на подготовке и проведении занятий.
![]()
Проведение быстрой и объективной проверки знаний учащихся.
![]()
Достижение максимальной понятности в изучении нового учебного материала.
![]()
Избавьтесь от необходимости подбирать задания и проверять их после уроков.
![]()
Улучшить дисциплину во время занятий.
![]()
Получить возможность творчески трудиться.
Просмотр материала учебного занятия «Запись урока по теме "Перемещение при прямолинейном равноускоренном движении", 9 класс»
Запись материала занятия по физике для учащихся 9 класса на тему: «Перемещение при прямолинейном равноускоренном движении»
Цели обучения: повторение, обобщение и закрепление основных понятий, терминов и формул, связанных с прямолинейным равноускоренным движением; ознакомление учащихся с выводом формулы проекции вектора перемещения для такого движения.
Воспитательные задачи: в рамках формирования научного мировоззрения ознакомить учащихся с понятием прямолинейного равноускоренного движения.
- Развитие навыков мобилизации и применения знаний для самостоятельного решения задач
- Развитие логического мышления
- Формулирование четких и лаконичных ответов на вопросы
- Развитие способностей к анализу и синтезу
- Выделение главного, выводы и выделение существенных признаков объектов
Формы работы учащихся: фронтальная и индивидуальная
Средства: компьютер, мультимедийный проектор, доска, учебник, журнал.
Методы: словесный, практический, объяснительно-иллюстративный.
1. Организационный момент
Приветствие учащихся. Знакомство с ними. Запись в классный журнал отсутствующих учеников. Сообщение темы урока. Запись ее на доске и в тетрадях учащихся.
2. Актуализация знаний.
Перед тем как мы продолжим изучение данного материала, давайте вспомним и повторим ранее изученное.
- Что означает термин "равномерное, прямолинейное движение"?
- Какую величину называют скоростью при равномерном движении?
- В каких единицах измеряется скорость?
- Каково соотношение между скоростью в километрах в час и метрах в секунду?
- Когда проекция скорости равномерного движения на ось положительна, а когда отрицательна?
После того, как я услышу ответы студентов, предложу им выполнить небольшую самостоятельную работу на листах. Используя график зависимости скорости движения тела от времени, они должны определить скорость тела в конце 5-ой секунды, предполагая, что характер его движения не изменяется. 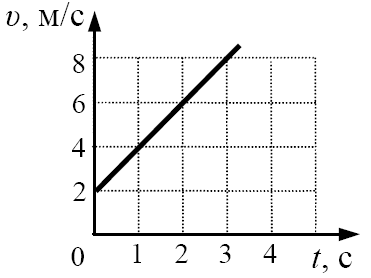 Начальная скорость составляет 2 м/с, а ускорение можно найти, рассматривая момент времени в 3 секунды. (8-2)/3=2 м/с^2. Затем они должны составить уравнение скорости тела, движущегося с начальной скоростью
Начальная скорость составляет 2 м/с, а ускорение можно найти, рассматривая момент времени в 3 секунды. (8-2)/3=2 м/с^2. Затем они должны составить уравнение скорости тела, движущегося с начальной скоростью 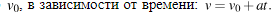 V=2+2*5=12
V=2+2*5=12
- 9 м/с
- м/с
- м/с
- м/с
С помощью графика зависимости скорости движения тела от времени определите его ускорение.
1) 6 м/с²
2) -6 м/с²
3) 1,5 м/с²
4) -1,5 м/с²
Решение: За четыре секунды скорость тела увеличилась на 6 м/с. Следовательно, ускорение тела равно 1,5 м/с²
С помощью графика зависимости скорости движения тела от времени определите его ускорение.
1) 2 м/c²
2) -2 м/c²
3) 8 м/c²
4) -8 м/c²
По прошествии четырех секунд скорость тела увеличилась на 8 м/сек. Следовательно, ускорение тела равно 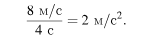
 4. Мотоциклист и велосипедист начинают движение из состояния покоя одновременно. Ускорение мотоциклиста в три раза больше, чем у велосипедиста.
4. Мотоциклист и велосипедист начинают движение из состояния покоя одновременно. Ускорение мотоциклиста в три раза больше, чем у велосипедиста.
Во сколько раз скорость мотоциклиста больше скорости велосипедиста в один и тот же момент времени? 1) в 1,5 раз 2) 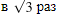 3) в 3 раза 4) в 9 раз Решение.
3) в 3 раза 4) в 9 раз Решение.
Так как и велосипедист, и мотоциклист начинают движение из состояния покоя, законы изменения их скоростей со временем выглядят следующим образом: 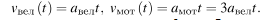 Таким образом, в любой момент времени скорость мотоциклиста в 3 раза больше скорости велосипедиста. Правильный ответ: 3. 3. Изучение нового материала Нам необходимо вывести формулу, с помощью которой мы могли бы рассчитывать проекцию вектора перемещения тела, движущегося прямолинейно и равноускоренно, за любой промежуток времени.
Таким образом, в любой момент времени скорость мотоциклиста в 3 раза больше скорости велосипедиста. Правильный ответ: 3. 3. Изучение нового материала Нам необходимо вывести формулу, с помощью которой мы могли бы рассчитывать проекцию вектора перемещения тела, движущегося прямолинейно и равноускоренно, за любой промежуток времени.
Получим информацию из изображения 14 на странице 29 вашего учебника. Как показано на рисунке 14а и рисунке 14б, отрезок AC представляет собой график проекции вектора скорости тела, двигающегося с постоянным ускорением а. Вопрос для обсуждения в классе: какая формула определяет вектор перемещения в случае прямолинейного равномерного движения тела (той же формулой, что и площадь под графиком проекции вектора скорости).
Какой вывод мы можем сделать? (проекция вектора перемещения численно равна площади этого прямоугольника). Докажем, что и в случае прямолинейного равноускоренного движения проекцию вектора перемещения можно определить по той же формуле, что и площадь фигуры, заключенной между графиком AC, осью Оt и отрезками ОА и ВС.
В данном случае проекция вектора перемещения численно равна площади под графиком скорости. Для этого на оси Ot (рис 14а) выделим небольшой промежуток времени db.
Из точек d и b проведем перпендикуляры к оси Ot до их пересечения с графиком проекции вектора скорости в точках a и c. Таким образом, за время отрезка db, скорость тела меняется от 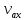
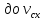 . За достаточно небольшое время проекция вектора скорости меняется очень незначительно, поэтому движение тела в течение этого времени почти не отличается от равномерного, т.е. от движения с постоянной скоростью.
. За достаточно небольшое время проекция вектора скорости меняется очень незначительно, поэтому движение тела в течение этого времени почти не отличается от равномерного, т.е. от движения с постоянной скоростью.
В данном случае участок AC графика можно рассматривать как горизонтальную полоску, а прямоугольник ACBD — как горизонтальную полоску. Таким образом, площадь этой полоски численно равна проекции вектора перемещения за промежуток времени, соответствующий отрезку DB. Вся площадь фигуры OACB можно разбить на такие полоски. Назовите, какую фигуру образуют эти полоски?
Следовательно, какова будет проекция вектора перемещения за промежуток времени, соответствующий отрезку OV? (площадь трапеции, которая определяется по той же формуле). Какова площадь трапеции? Используя рисунок 14б, найдем основания и высоту трапеции. Скажите, как их можно назвать.
АО=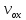 , ВС=
, ВС=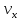 , ОВ=t , С учетом этой информации можем вывести формулу для нахождения площади трапеции. Таким образом:
, ОВ=t , С учетом этой информации можем вывести формулу для нахождения площади трапеции. Таким образом: 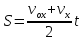 (1) Вспомним, как выглядит скорость при равномерном равноускоренном движении?
(1) Вспомним, как выглядит скорость при равномерном равноускоренном движении?
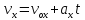 Учитывая, что S=Sx, мы можем переписать формулу (1) в другом виде. Каждый студент записывает эту формулу в свою тетрадь и проверяет ее с той, которую преподаватель показывает на доске. Таким образом, мы получаем формулу для расчета проекции вектора перемещения при равноускоренном движении.
Учитывая, что S=Sx, мы можем переписать формулу (1) в другом виде. Каждый студент записывает эту формулу в свою тетрадь и проверяет ее с той, которую преподаватель показывает на доске. Таким образом, мы получаем формулу для расчета проекции вектора перемещения при равноускоренном движении.
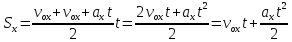
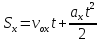 С помощью этой формулы можно вычислить проекцию вектора перемещения при движении тела со скоростью, уменьшающейся по модулю, в этом случае векторы скорости будут направлены в разные стороны и их проекции будут иметь противоположные знаки. На видеофрагменте демонстрируется равноускоренное прямолинейное движение.
С помощью этой формулы можно вычислить проекцию вектора перемещения при движении тела со скоростью, уменьшающейся по модулю, в этом случае векторы скорости будут направлены в разные стороны и их проекции будут иметь противоположные знаки. На видеофрагменте демонстрируется равноускоренное прямолинейное движение.
Задания для учеников на демонстрацию. 4. Фиксация учебного материала. Решение задач. Рымкевич №53 Сколько времени потребуется автомобилю, чтобы увеличить свою скорость с 12 м/с до 20 м/с, если его ускорение составляет 0,4 м/с 2? 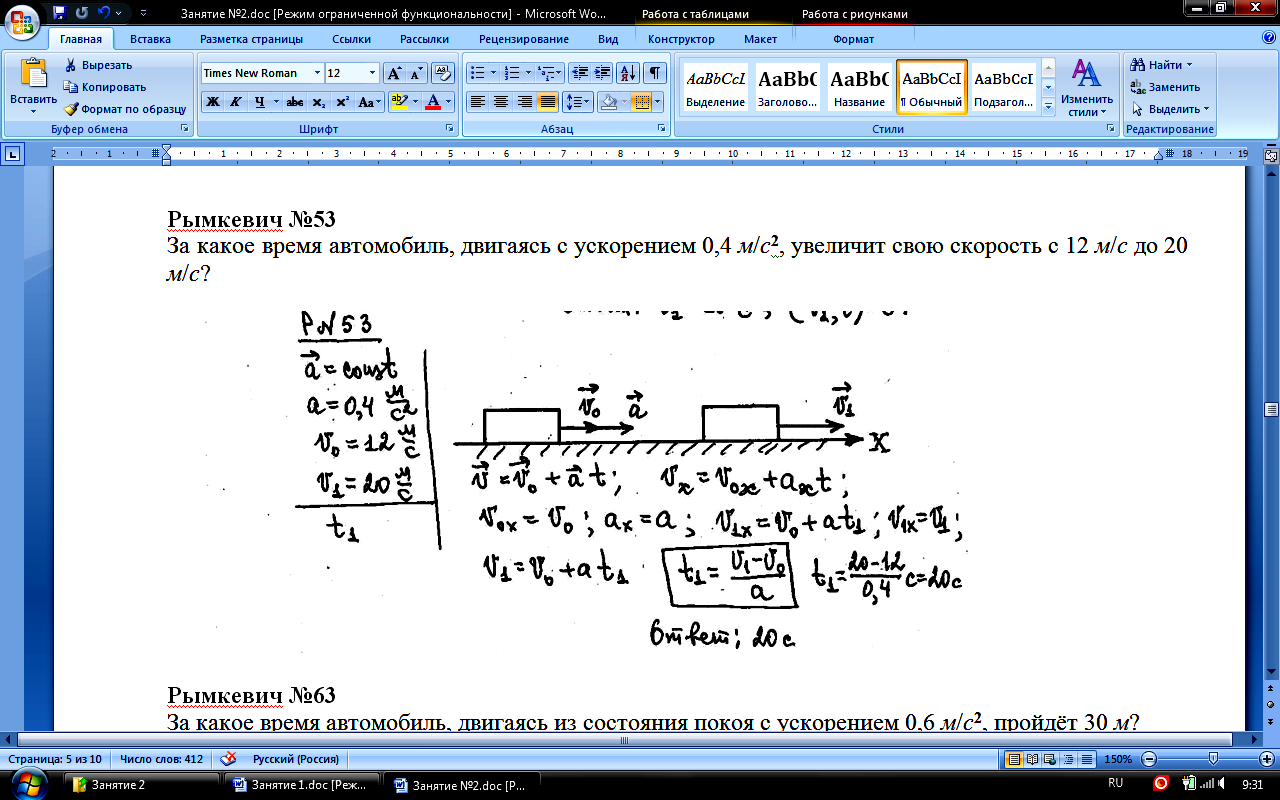 Задача №2. Велосипедист съехал с горки за 5 с, имея постоянное ускорение 0,5
Задача №2. Велосипедист съехал с горки за 5 с, имея постоянное ускорение 0,5 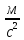 .
.
Найти длину горки, если известно, что в начале скорость велосипедиста была 18 км/ч.
Дано: t=5c 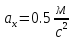 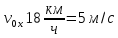 Найти Найти 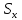 | 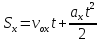 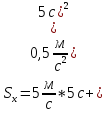 |


