Ускорение в равномерно движущемся прямолинейном движении (РПД) равно нулю, так как скорость тела остается постоянной на протяжении всего движения. В этом случае отсутствует изменение скорости, а значит, и ускорение, как физическая величина, равно 0 м/с².
Таким образом, при равномерном движении на прямой линии не происходит ни ускорения, ни замедления, и тело движется с постоянной скоростью, определяемой начальными условиями движения.
Чему равно ускорение в рпд
Не существует такого понятия как "отрицательное ускорение". Когда движущееся тело замедляет свою скорость, начинает действовать 3-й закон Ньютона: F/m равно или больше S/tt. Ньютон пытался сравнять ускорения S/tt и F/m, но ошибка в формуле S=att/2 не позволяла ему это сделать. Он допустил эту ошибку, когда искал ускорение свободного падения "яблока".
Конечная скорость (9,8) это НЕ at! at — это СРЕДНЯЯ скорость! Она равна (0+V конечная)/2. V средняя=at.
Vконечная=2at. S=(0+2at)/2*t. S=att (и-НИКАКИХ " /2)! ..Если тело весом (массой) m кг., прошло путь S за время t, то ускорение S/tt=F/m. Искать просто ускорение-бессмысленно. Оно должно помочь найти S,t,F,m,V
Задача: камень весом 25 кг. передвинули на 40 метров за минуту.
Изучение законов природы
Главный вопрос: какую силу мы приложили (F) ? Ответ: 40/3600=F/25. Получаем: 0,28 км.м/с. («крутящий момент») Задача: этот-же камень, с таким же упорством, был перетащен на расстояние …100 м. Главный вопрос: где t ? Ответ: 100/tt=0,28/25. Получаем: 1,5 минуты (95 секунд). Нужно пересмотреть «законы» Ньютона… (при равномерном движении — НЕТ ускорения. А ЧТО со СРЕДНЕЙ скоростью?
А из неё мы можем найти ускорение!) При решении задач нельзя вычитать «скорость из скорости». Любое движение — это энергия и время. Оба этих понятия не могут быть отрицательными. Время не возвращает назад. И =Энергия.
Она либо присутствует, либо отсутствует. S/tt=F/m — это означает, что материя со временем превращается в энергию, а энергия со временем превращается в материю. ПРИРОДА- ВЕЧНА !
Администратор :
Спасибо за альтернативный взгляд, который не был включен в учебники физики. Надеюсь, это поможет учащимся расширить свои знания в области физики.
Василий :
Изменение скорости — это вектор, который не может быть отрицательным. Однако проекция ускорения может быть отрицательной. Я не согласен с вашими словами, они кажутся нелепыми. По крайней мере потому, что at обозначает изменение скорости, а средняя скорость вычисляется как отношение пройденного пути к времени движения, или пути к времени движения, если речь идет о средней ПУТЕВОЙ скорости. Деление на 2 в уравнении движения происходит из-за правил интегрирования, которые говорят, что интеграл at по dt равен 0.5at^2
иван шкинёв :
Если тело пройдет расстояние S за время t, то график движения не влияет ни на среднюю скорость, ни на ускорение. Это означает, что изменение скорости не всегда зависит от движения. При равномерном движении ускорение такое же, как и при любом другом движении, так как ускорение эквивалентно затраченной на движение энергии и изменению скорости. S/tt — это изменение скорости.
Но F/m — это энергия! И она влияет на изменение скорости, измеряется как "м/сек.сек." При решении задач на движение необходимо перевести движение в среднюю скорость и искать ускорение из нее. У "яблока…" V нач.=0, V конеч.=9,8 м/с. V средняя=(0+9,8):2 V ср.=4,9 м/сек. S=V средняя (!)*t.
Произведение 4,9*1=4,9 метра. "Средняя скорость" представлена как "at" (в любом графике движения). "Конечная" скорость равна 2ат. S=(0+2ат)/2*t. S=ат^2, или at*t. Задача: V начальная = 10 м/сек. V конечная = 50 м/сек. t=10 секунд.
S=? а=?
Решение: Грубая ошибка: нахождение "а": (50-10)/10. "а"=4 м/секунда^2. S=ат^2. 4*100=400 метров. Правильно будет так: (10+50)/2=30 м/сек. Это-средняя скорость. "а"=30/10. a=3 м/секунда^2.
S=: V средняя*t=300 метров; а*tt. 3*100=300 метров S/tt=F/m. Ньютон должен был вывести такую формулу, но из-за ошибки "атт/2" не смог. S=ат^2 = (at*t). (не "заморачивай-те" головы студентов интегралами).
иван шкинёв :
S/tt=F/m. Как связаны эти части равенства? Обратите внимание на то, что F и m связаны с помощью "а". Задача: масса машины m=1165 кг. Мощность мотора= 75 л.с. («Москвич», «Жигули»). Вопрос: за какое время машина достигнет скорости 100 км/час.
Сколько времени машина минимально пройдет 150 м, 250 м., 400 м. Какую скорость она достигнет за 10 сек, за 15 сек., за 25 сек.?
Решение: F/m=a. кпд двигателя=16%.
75 л.с=5625 кг.м/с 16% будет: 5625/6,25=900 кг.м/сек. Это 12 л.с. (при 100% кпд) a=F/m. 900/1165=0,77 м/сек.сек. Это «ускорение» F/m — «ЭНЕРГИЯ движения» Скорость 100 км/час (27,7 м/с машина достигает за 18 сек.) a=V средняя/t. 13,9/18=0,77 м/сек.сек. «УСКОРЕНИЕ ОДИНАКОВО и через ЭНЕРГИЮ «at» и через «прибавку скорости к скорости» -скорость машины через 10 сек.: V кон.=2at.
Указаны скорости в м/с и км/ч для различных интервалов времени: 10 секунд, 15 секунд и 25 секунд. При этом также рассчитаны расстояния, которые машина пройдет за определенный промежуток времени. Для вычисления максимальной скорости машины использовано ускорение и время.
Мурат :
Что означает ошибка att/2 и почему она считается ошибкой? Вы обосновали свои теории об энергии, но не объяснили, почему att/2 — ошибка. Я не очень силен в физике, поэтому описал все, как смог.
Аноним :
Халид :
Тело движется с постоянной силой 12 Н, а его зависимость координаты от времени выражена уравнением: (м). Необходимо определить массу тела, импульс тела в момент времени t = 2 c и среднюю скорость за промежуток времени от t1 = 0 c до t2 = 2 c.
S/tt=F/m. Необходимо выяснить, двигалось ли тело или стояло на месте?
Зависимость координаты тела от времени в СИ: х = –15 + 2,5t. Какова скорость и направление движения тела? Через какое время координата тела станет равной 15м?
Аноним :
Исходя из уравнения, скорость тела равна 2,5 м/с и направлена в положительную сторону оси, что означает движение вперед. Чтобы найти время, через которое координата станет равной 15, подставляем число 15 и находим время. Х=-х0+Vt (X+xo)/V=t-это рабочая формула для нахождения времени 15+15:2,5=t 12=t
Иван Шкинёв:
При решении задач на «равномерное движение с начальной скоростью больше (или меньше 0) искать «а» нужно со всего пути, а не только с момента V начальной скорости. Если машина прошла 100 км и только один раз ускорилась в течение 10 секунд, то это не значит, что она израсходовала бензин только на разгон. Даже в космосе, в невесомости, она когда-нибудь остановится, постепенно снижая скорость.
Значит: её движение не является равномерным. Если бы она продолжала двигаться равномерно, её «ускорение» — энергия движения — снизилась бы в t квадрат раз: (а=10 м/сс…а=0,1 м/сс…а=0,0000……м/сек.сек…..) Задача: V начальная скорость = 10 м/с, «а» = 2 м/сек.сек, t = 5 сек. S-? «а»=?
Решение: ….(если будем рассматривать «а» только с момента нарастания скорости, то «а» не надо искать. Оно = 2 м/сек.сек.
Вот, весь путь ускорение меняется: a=S/tt (без 2S !). h (V конечная) треугольника=2at. 2*2*5=20 м/сек. Общая конечная скорость=10+20. Получилась трапеция, площадь которой-(путь)= (v+v+2at)/2*t. (10+10+20)/2*5. S=100 м. а=100/25=4 м/сек.сек. (или считать V ср./t 20/5=4 м/сек.сек.
Не забывайте и не путайте: at- это средняя скорость. 2at- это конечная скорость. (при V нач.=0) И ещё: Средняя скорость и ускорение не зависят от графика движения тела! Средняя скорость-это равномерное движение. Скорость at-это то-же равномерное движение, V нач.=V конечной..
Если начальная и конечная скорости не равны- это не скорость at, и не средняя скорость…. …Ошибка в формуле S=att/2 привела к этой белеберде, к интегралам. S/t=at, a at*t=2S (!?). "яблоко…": 4,9/1=4,9. 4,9/1=9,8 ?! S,t.m…можно измерить. Задача-найти F ! S/tt=F/m. Вот таким должен был быть труд Ньютона.
Однако, ошибка «/2….» …мощность двигателя в соответствии с условиями задачи. (вес автомобиля…1200 кг) ..автомобиль имеет ускорение 4 м/сс.. (для автомобиля это считается «приличным» ускорением..) F/1200=4 сек.сек. F=4800 кг м./сек. Это=64 л.с. при 100% КПД КПД ДВС=16%. 64*6,25=400 л.с. (существуют такие двигатели. Хотя вес УКАЗАННЫХ автомобилей составляет 2,5-3 тонны…) Вот пример «теории и практики».
А если вес автомобиля …2650 кг., то мотор должен быть: 4*2650/75*6,25=883 л.с.
Формулы для равноускоренного движения
Ускорение при равноускоренном движении можно найти по формуле: a = (v — v0) / t
Здесь v0 — начальная скорость, a — ускорение, t — время движения.
График зависимости скорости от времени при равноускоренном движении представляет собой прямую линию. Попробуйте пройти небольшой тест для закрепления знаний.
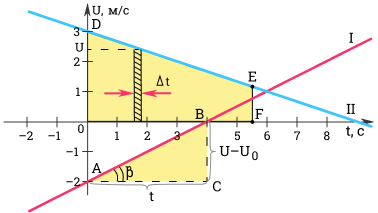
Как можно определить ускорение? Одним из способов является использование угла наклона графика скорости. На приведенной выше диаграмме модуль ускорения определяется отношением сторон треугольника ABC. Вот формула ускорения в физике.
а = v — v 0 t = B C A C
Чем больше угол β, тем круче (больше наклон) график относительно оси времени. Следовательно, ускорение тела будет больше.
Для первого графика: v 0 = -2 м/c; а = 0,5 м/с^2.
Для второго графика: v 0 = 3 м/с; а = -13 м/с^2.
Исходя из данной диаграммы, физик также может вычислить (определить) перемещение тела за время t. Как это можно сделать?
Давайте разделим все время t на бесконечно маленькие интервалы ∆ t . Перемещение s за время t будет равно площади трапеции O D E F .
s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v — v 0 ) 2 t .
Мы знаем, что v — v 0 = a t , поэтому окончательная формула или расчет для перемещения тела будет выглядеть так:
s = v 0 t + a t 2 2
Для того чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение (расстояние). Изменение координаты в зависимости от времени выражает закон равноускоренного движения.
Какова будет формула пути при равноускоренном движении? В этом случае путь изменяется согласно квадратной зависимости: 8=v0t + at²/2.
Закон равноускоренного движения
Формула равноускоренного движения: y = y 0 + v 0 t + a t 2 2 .
Еще одна типичная задача по кинематике — найти координаты при известных начальной и конечной скоростях и ускорениях.
Исключив из уравнений выше время и решив их, получаем: s = v 2 — v 0 2 2 a .
При известных начальной скорости, ускорении и перемещении можно найти конечную скорость объекта: v = v 0 2 + 2 a s .
Если v 0 = 0, то s = v 2 2 a и v = 2 a s
Величины v , v 0 , a , y 0 , s , используемые в выражениях, являются численными значениями. Они могут быть как положительными, так и отрицательными — это зависит от характера движения и направления координатных осей в конкретной задаче.
Направление вектора ускорения
Не всегда направление вектора ускорения совпадает с направлением вектора скорости!
Равноускоренным движением называется движение, в котором скорость изменяется на одинаковую величину за одинаковые промежутки времени. При этом направления векторов скорости и ускорения тела совпадают (а ↑↑ v).
Равнозамедленное движение — это особый случай равноускоренного движения, при котором скорость уменьшается на одинаковую величину за одинаковые промежутки времени. При этом направления векторов скорости и ускорения тела противоположны друг другу (а ↑↓ v).
Живой пример №2. Машина вначале ускорилась, а затем замедлила своё движение. Когда она разгонялась, направления векторов скорости и ускорения совпадали, так как скорость увеличивалась. Но когда она затормозила, скорость уменьшилась, потому что вектор ускорения изменил своё направление на противоположное.

График ускорения
График ускорения представляет собой зависимость проекции ускорения от времени. При равноускоренном прямолинейном движении проекция ускорения остается постоянной (ax=const). График ускорения при таком движении представляет собой прямую линию, параллельную оси времени.

Зависимость местоположения графика проекции ускорения относительно оси Х от направления вектора ускорения:
- При расположении графика выше оси времени, движение является равноускоренным (направление вектора ускорения совпадает с направлением оси Х). На рисунке выше тело 1 движется равноускоренно.
- При расположении графика ниже оси времени, движение является равнозамедленным (вектор ускорения направлен противоположно оси Х). На рисунке выше тело 2 движется равнозамедленно.
Если график ускорения расположен на оси времени, движение является равномерным, так как ускорение равно 0. Скорость в этом случае остается постоянной.

Для сравнения модулей ускорений по графикам необходимо проанализировать их удаленность от оси времени, независимо от того, находятся ли они выше или ниже этой оси. Чем дальше от оси находится график, тем больше его модуль. На изображении график 2 находится дальше от оси времени, чем график 1. Следовательно, модуль ускорения тела 2 больше, чем ускорения тела 1.
Пример №3. По графику проекции ускорения необходимо найти участок, на котором тело двигалось равноускоренно. Также нужно определить ускорение в момент времени t1 = 1 и t2 = 3 с.

С начала до первой секунды ускорение возрастало, затем оставалось постоянным до второй секунды, и после этого начало уменьшаться до четвертой секунды. Поскольку в равноускоренном движении ускорение должно быть постоянным, соответствующий этому условию участок графика находится с 1 по 2 секунду.
Для определения ускорения в момент времени t нужно провести перпендикулярную прямую через соответствующую точку времени t. Затем нужно провести перпендикуляр к оси ускорения через точку пересечения с графиком. Значение точки, в которой пересекается перпендикуляр с этой осью, и будет показывать ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с 2 . В момент времени t2 = 3 ускорение a = 0 м/с 2 .
Текст: Алиса Никитина, 18.4k
EF18774 — это номер задания, который необходимо выполнить.

Иллюстрация отображает кривую, описывающую зависимость координаты x от времени t для тела, движущегося вдоль оси Ох (парабола). Графики А и Б отражают зависимости физических параметров движения этого тела от времени t. Определите соответствие между графиками и физическими величинами, которые эти графики могут представлять.
Сопоставьте каждой позиции на графике соответствующее утверждение и запишите цифры в поле в порядке АБ.

Алгоритм проблемы
- Необходимо определить, какая форма движения соответствует графику координаты тела от времени.
- Требуется найти величины, которые характеризуют данное движение.
- Необходимо определить изменения в величинах, характеризующих данное движение.
- Установить соответствие между графиками А и Б и величинами, описывающими движение.
Решение проблемы
График зависимости координаты тела от времени выглядит как парабола в случае равноускоренного движения. Поскольку движение тела происходит относительно оси Ох, траектория представляет собой прямую. Равноускоренное прямолинейное движение характеризуется следующими параметрами:
- пройденное расстояние и положение;
- скорость;
- ускорение.
Как изменяются перемещение и путь при равноускоренном прямолинейном движении, так же изменяется и координата тела. Их графики зависимости от времени также представляют собой параболы.
График зависимости скорости от времени в случае равноускоренного прямолинейного движения является прямой линией, которая не может быть параллельна оси времени.
График зависимости ускорения от времени при таком движении представляет собой прямую линию, перпендикулярную оси ускорения и параллельную оси времени, так как в этом случае ускорение является постоянной величиной.
Исходя из этого, ответ "3" исключается, остаётся проверить ответ "1". Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола, поэтому ответ "1" также не подходит.
Один из графиков представляет собой прямую линию, которая идет параллельно оси времени и связана с зависимостью ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
Другой график также является прямой линией, но она не параллельна оси времени. Мы установили, что этот график соответствует зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Задание EF17992
Автомобиль начал движение со скоростью 5 м/с и ускорением. Когда он проехал 40 метров, его скорость увеличилась до 15 м/с. Какое ускорение получил автомобиль?
Шаги для решения задачи
- Запишите известные данные.
- Найдите формулу, которая связывает известные величины.
- Найдите искомую величину, выразив ее из формулы.
- Вычислите искомую величину, подставив известные данные в формулу.
Решение
Запишем известные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, связывающая ускорение и пройденный путь:

Поскольку скорость увеличивается, ускорение имеет положительное значение, поэтому мы добавим знак "+" перед ним в формуле.
Давайте выразим ускорение из этой формулы:

Подставим уже имеющиеся значения и произведем расчет скорости движения автомобиля:

Задание EF18202
Тщательно изучите представленное задание и выберите правильный вариант из перечня. На изображении показан график зависимости компоненты скорости тела vx от времени.

Какой из следующих графиков соответствует графику зависимости ускорения тела по оси х от времени в интервале от 6 до 10 секунд?
Подход к решению
- Описать движение тела на участке графика, указанном в условии задачи.
- Рассчитать ускорение движения тела на данном участке.
- Выбрать график, соответствующий графику зависимости ускорения тела от времени.
Решение
Согласно графику проекции скорости в интервале от 6 до 10 секунд тело двигалось равномерно замедленно. Это означает, что проекция ускорения по оси Ох отрицательная. Поэтому ее график должен находиться ниже оси времени, и варианты "а" и "в" являются неверными.
Чтобы выбрать между вариантами "б" и "г", необходимо вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Для расчетов применим данное выражение:

Добавим в нее информацию, которая нам известна, и проведем расчеты:

Диаграмма "г" соответствует данному значению.
Задание EF18027
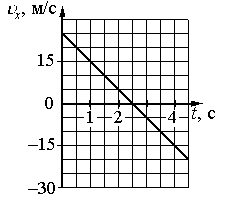
На диаграмме изображена зависимость проекции скорости тела от времени при его движении вдоль оси x. Необходимо определить значение ускорения тела.
Алгоритм решения
- Запишем формулу ускорения.
- Запишем формулу для расчета модуля ускорения.
- Выберем произвольные 2 точки на графике.
- Определим значения времени и проекции скорости для этих точек (получим исходные данные).
- Подставим данные в формулу и рассчитаем ускорение.
Решение
Запишем формулу ускорения:

Для решения поставленной задачи необходимо вычислить модуль ускорения, итак, формула имеет следующий облик:

Выбираем две точки на графике. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Вставляем данные в формулу и находим значение ускорения:
Формулы прямолинейного равноускоренного движения
Важные параметры движения тела в кинематике — это ускорение, скорость и координата. Рассмотрим формулы этих параметров для прямолинейного равноускоренного движения.

Для описания движения необходимо выбрать систему отсчёта. Если речь идет о прямолинейном движении, то удобно выбрать такую систему отсчёта, у которой ось координат параллельна направлению движения. В этом случае мы сразу можем перейти от векторного представления к проекциям.
Напомним, что в случае равноускоренного движения ускорение постоянно, поэтому:
Если нам нужно выразить скорость через время, то мы можем использовать формулу ускорения, которую мы уже упоминали. Умножив обе части на $t$ и перенеся известные значения вправо, мы получим:
Чтобы выразить формулу для координаты, нужно помнить, что пройденное расстояние можно найти на графике скорости. Оно равно площади, заключенной между графиком скорости и осью времени.
Из формулы скорости можно увидеть, что она описывает прямую зависимость. График этой зависимости представляет собой прямую линию с некоторым наклоном, который зависит от коэффициента $a$.
Под этой линией находится трапеция с высотой $t$ и основаниями $v$ и $v_0$. Согласно геометрии, площадь трапеции равна полусумме оснований, умноженной на высоту:
Учитывая, что в начальный момент координата была равна $x_0$, и подставляя полученное значение $v$, мы окончательно получаем формулу координаты равноускоренного прямолинейного движения:
Информацию о движении с постоянным ускорением удобно представить в виде табличных данных:

Скорость. Ускорение. Равноускоренное прямолинейное движение
1. Неравномерное движение — это движение со скоростью, меняющейся со временем.
Если скорость движения меняется в течение времени, то говорят, что это неравномерное движение.
При неравномерном движении уже нельзя использовать формулу (x=x_0+v_xt), так как скорость движения не постоянна. Поэтому для описания изменения положения тела со временем при неравномерном движении вводится средняя скорость.
Средней скоростью неравномерного движения называется величина, равная отношению перемещения тела к времени: (v=frac{vec}{t}).
Выражение, записанное в формуле, определяет среднюю скорость в качестве векторной величины. Для практических целей использование этой формулы может быть применено для определения модуля средней скорости только в том случае, если тело движется вдоль прямой в одном направлении. Однако, если необходимо определить среднюю скорость движения автомобиля из Москвы в Санкт-Петербург и обратно для расчета расхода топлива, то данную формулу нельзя использовать, так как в этом случае перемещение равно нулю, и средняя скорость также равна нулю. Поэтому на практике для определения средней скорости используется величина, которая равна отношению пройденного пути (l) к времени (t): (v_=frac). Эту скорость обычно называют средней путевой скоростью.
2. Важно понимать, что зная среднюю скорость неравномерного движения на участке траектории, нельзя точно определить положение тела в любой момент времени. Например, если средняя скорость автомобиля за 2 часа составляет 50 км/ч, то нельзя точно сказать, где он будет через 0,5 часа, 1 час, 1,5 часа и т.д. Ибо он мог двигаться с различными скоростями и даже стоять на протяжении различных промежутков времени.
3. Проходя по траектории, тело затрагивает все её точки по порядку. В каждой точке траектории оно имеет своё положение и определённую скорость в конкретный момент времени.
Мгновенной скоростью называется скорость тела в определённый момент времени в конкретной точке траектории.
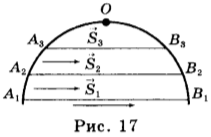
При уменьшении перемещения и соответственно времени движения тела до очень маленьких значений, например, спидометр перестанет регистрировать изменения скорости, и движение в течение этого короткого промежутка времени можно считать равномерным. Таким образом, средняя скорость на этом участке является мгновенной скоростью тела в данной точке.
Мгновенная скорость — это физическая величина, равная отношению малого перемещения ( ( Delta> ) ) к малому промежутку времени ( Delta ) , за которое это перемещение произошло: ( vec=frac><Delta> ) .
4. Равноускоренным движением называется движение, при котором скорость тела изменяется на одно и то же значение за любые равные промежутки времени.
Выражение "любые одинаковые интервалы времени" означает, что независимо от того, какие одинаковые интервалы времени (2 с, 1 с, доли секунды и т. д.) мы возьмем, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.
5. Особенностью равноускоренного движения, помимо скорости и перемещения, является ускорение.
Допустим, в начальный момент времени ( t_0=0 ) скорость тела равна ( vec_0 ) . В некоторый момент времени ( t ) она стала равной ( vec ) . Изменение скорости за промежуток времени ( t-t_0=t ) равно ( vec-vec_0 ) (рис.18). Изменение скорости за единицу времени равно: ( frac<vec-vec_0> ) . Это и есть ускорение тела, она характеризует скорость изменения скорости ( vec=frac<vec-vec_0> ) .
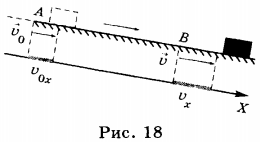
Ускорение векторной физической величины тела при равноускоренном движении равно отношению изменения скорости тела к промежутку времени, за который произошло это изменение.
Единица ускорения равна 1 м/с². Такое ускорение происходит, когда скорость тела изменяется за 1 с на 1 м/с.
Направление ускорения зависит от изменения скорости тела: если скорость увеличивается, ускорение направлено в том же направлении, если скорость уменьшается, ускорение направлено противоположно.
Преобразовав формулу ускорения, можно получить выражение для скорости тела при равноускоренном движении: (vec{v}=vec{v_0}+vec{at}). Если начальная скорость тела (v_0=0), то (vec{v}=vec{at}).
Для нахождения скорости равноускоренного движения в конкретный момент времени нужно записать формулу для проекции скорости на ось ОХ. Она выглядит так: ( v_x = v_0 + a_xt ) ; если ( v_0 =0 ) , то ( v_x = a_xt ) .
7. Как можно заметить из уравнения скорости равноускоренного движения, она линейно зависит от времени. График зависимости модуля скорости от времени является прямой линией, образующей определенный угол с осью абсцисс (ось времени). На рисунке 19 показаны графики зависимости модуля скорости от времени.
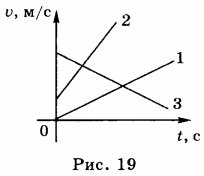
График 1 иллюстрирует движение объекта без начальной скорости, но с ускорением, направленным в том же направлении, что и скорость. График 2 показывает движение с начальной скоростью ( v_ ) и ускорением, направленным также, как и скорость. График 3 отображает движение с начальной скоростью ( v_ ) и ускорением, направленным в противоположную сторону от направления скорости.
8. На рисунке представлены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).
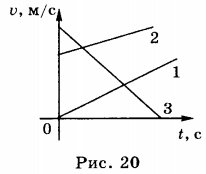
График 1 отражает движение с ускорением вдоль положительного направления оси X при отсутствии начальной скорости; график 2 показывает движение с начальной скоростью ( v_ ) , при этом и ускорение, и скорость направлены вдоль положительного направления оси X; график 3 описывает движение с начальной скоростью ( v_ ) : до момента времени ( t_0 ) направление скорости совпадает с положительным направлением оси X, ускорение же направлено в противоположную сторону. В момент времени ( t_0 ) скорость равна нулю, после чего и скорость, и ускорение направлены в сторону, противоположную положительному направлению оси X.
9. На рисунке 21 изображены графики зависимости проекции ускорения равноускоренного движения от времени.
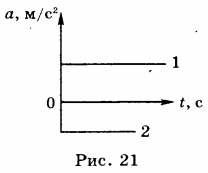
График 1 отображает движение с положительной проекцией ускорения, а график 2 показывает движение с отрицательной проекцией ускорения.
10. Формула для перемещения тела в равноускоренном движении может быть получена из графика зависимости проекции скорости этого движения от времени (рис. 22).
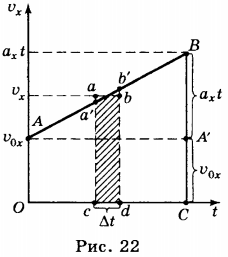
Пусть на графике выделен небольшой отрезок ( ab ) , от которого проведены перпендикуляры из точек ( a ) и ( b ) на ось абсцисс. Если промежуток времени ( Delta ) , соответствующий отрезку ( cd ) на оси абсцисс, невелик, то скорость можно считать постоянной, и тело движется равномерно. В этом случае фигура ( cabd ) почти не отличается от прямоугольника, и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку ( cd ) .
Такими полосками можно разбить всю фигуру ОАВС, и её площадь будет равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время ( t ) численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: ( S_x= frac(OA+BC)OC ) .
Этот математический выражение дает возможность определить местоположение (координату) объекта в любой момент времени, если известны начальная скорость, начальная координата и ускорение.
11. В реальной жизни часто применяются формулы вида ( v^2_x-v^2_=2a_xs_x ) или ( v^2-v^2_=2as ).
Если начальная скорость объекта равна нулю, то: ( v^2_x=2a_xs_x ).
Этот уравнение позволяет вычислить тормозной путь транспортных средств, то есть расстояние, которое проезжает, например, автомобиль до полной остановки. При определенном ускорении, которое зависит от массы автомобиля и мощности двигателя, тормозной путь увеличивается с увеличением начальной скорости автомобиля.
ПРИМЕРЫ ЗАДАНИЙ
1. На изображении изображены линии, изображающие зависимость пути и скорости объекта от времени. Какой из графиков представляет равноускоренное движение?
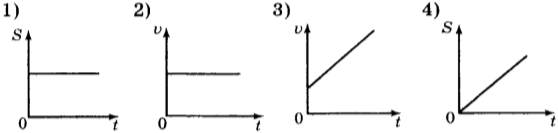
2. Автомобиль, начавший движение из состояния покоя на прямолинейной дороге, за 10 секунд приобрел скорость 20 м/с. Каково ускорение автомобиля?
1) 200 м/с 2 2) 20 м/с 2 3) 2 м/с 2 4) 0,5 м/с 2
3. На рисунках изображены графики зависимости координаты от времени для четырех тел, движущихся вдоль оси (Ox). У какого из тел в момент времени (t_1) скорость движения равна нулю?
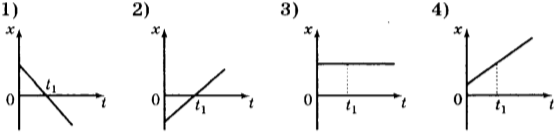
4. Графическое изображение показывает, как меняется проекция ускорения от времени для объекта, который движется вдоль оси ( Оx ) ).
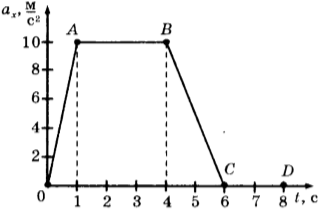
Для определения равноускоренного движения измерялись пройденные телом расстояния в последовательные моменты времени. Полученные результаты представлены в таблице.
1) только ОА 2) только АВ 3) только ОА и ВС 4) только CD
5. Скорость равноускоренного движения соответствует участку

Какое расстояние проходит тело за третью секунду?
1) 4 м 2) 4,5 м 3) 5 м 4) 9 м
6. На диаграмме показаны кривые зависимости скорости от времени для четырех тел, движущихся по прямой.
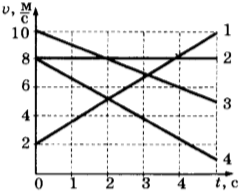
Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?
1) только 1 2) только 2 3) только 4 4) 3 и 4
7. По графику зависимости скорости тела от времени определите его ускорение.
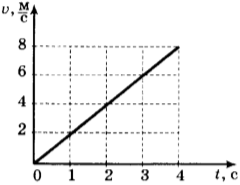
1) Скорость в момент времени 1 сек: 1 м/с 2) Скорость в момент времени 2 сек: -1 м/с 3) Скорость в момент времени 3 сек: 2 м/с 4) Скорость в момент времени 4 сек: -2 м/с
8. При изучении равноускоренного движения скорость тела измерялась в определённые моменты времени. В таблице приведены полученные данные. Найдите скорость тела в момент времени 3 секунды.

1) 0 м/с 2) 2 м/с 3) 4 м/с 4) 14 м/с
9. Графики показывают, как меняется скорость четырёх объектов со временем. Узнайте, у какого тела ускорение составляет -1,5 м/с?
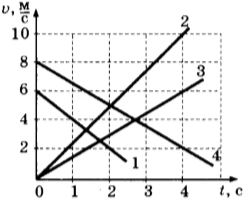
10. Путем анализа графика зависимости скорости тела от времени, установите скорость тела в конце 30-й секунды. Предполагается, что движение тела остается постоянным.
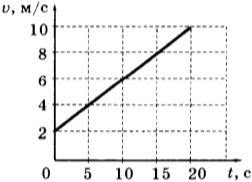
1) 14 м/с 2) 20 м/с 3) 62 м/с 4) 69,5 м/с
11. Два объекта двигаются вдоль оси ( Oх ) . На изображении показаны графики зависимости проекций скорости движения объектов 1 и 2 от времени.
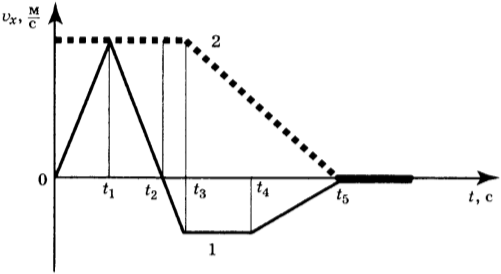
Выберите два правильных утверждения, используя данные графика. Укажите их номера.
1) В интервале времени ( t_3-t_5 ) тело 2 движется равноускоренно. 2) К моменту времени ( t_2 ) от начала движения тела прошли одинаковые расстояния. 3) В интервале времени ( 0-t_3 ) тело 2 находится в покое. 4) В момент времени ( t_5 ) тело 1 останавливается. 5) В интервале времени ( t_3-t_4 ) ускорение ( a_x ) тела 1 отрицательно.
12. График показывает зависимость проекции скорости от времени для тела, движущегося вдоль оси Ох.
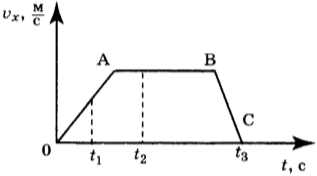
Выберите два верных утверждения, используя данные графика. Укажите их номера:
1) Отрезок ОА соответствует ускоренному движению объекта. 2) Отрезок AВ означает состояние покоя объекта. 3) В момент времени ( t_1 ) объект имело максимальное ускорение по модулю. 4) Момент времени ( t_3 ) соответствует остановке объекта. 5) В момент времени ( t_2 ) объект имело максимальное ускорение по модулю.
Определение 3
Равноускоренное движение представляет собой перемещение тела, при котором его скорость за одинаковые промежутки времени меняется одинаково — либо увеличивается, либо уменьшается.
В равноускоренном движении скорость не остается постоянной на протяжении всего пути. В этом случае наблюдается ускорение, которое приводит к постоянному увеличению скорости. Ускорение остается постоянным, но скорость увеличивается равномерно.
Помимо равноускоренного движения существует также равнозамедленное, где модуль скорости равномерно уменьшается. Таким образом, равноускоренное движение может происходить в различных измерениях, таких как:
- одномерное;
- многомерное.
В случае первого — движение осуществляется вдоль одной оси, в случае второго могут учитываться и дополнительные измерения.
Ускорение тела
Использование формул перемещений в случае равноускоренного движения и формул ускорения без учета времени возможно в различных плоскостях. Это может быть использовано, например, при расчете падения твердых тел в свободном падении и места падения. Это также применимо при точных и геометрических расчетах.
В отличие от равномерного движения, неравномерное движение происходит с разной скоростью вдоль каждой траектории. Чем же особенно неравномерное движение? Особенность заключается в том, что оно "равно ускоряется".
Мы связываем ускорение с увеличением скорости. Если скорость увеличивается равномерно, то это означает равномерное увеличение скорости. Как определить, увеличивается ли скорость равномерно? Для этого нам нужно измерить время и оценить скорость за одинаковый промежуток времени, используя формулы ускорения при равноускоренном движении.
Пример 1
Давайте представим, что автомобиль начал движение. В течение первых 2 секунд он разогнался до 10 м/с, затем за следующие 2 секунды достиг скорости 20 м/с, и еще через 2 секунды он уже двигался со скоростью 30 м/с. Скорость увеличивается на 10 м/с каждые 2 секунды, что и означает равномерное ускорение.
Ускорение определяет, насколько быстро изменяется скорость. Нужно также обратить внимание на формулу скорости в случае равномерного ускоренного движения.
Если скорость уменьшается, это замедленное движение. Но физики называют любое движение с изменяющейся скоростью ускоренным. Когда автомобиль начинает движение (скорость увеличивается) или замедляется, он все равно движется с ускорением.
Формула для расчета ускорения при решении задач
Для расчета ускорения тела, движущегося равномерно и прямолинейно, мы будем применять следующее уравнение, в которое входят проекции векторов ускорения и скорости:
Тут $a_x$ — это проекция ускорения на ось OX, которую мы и будем искать, $upsilon_x$ — проекция текущей скорости на ось OX, $upsilon_$ — проекция начальной скорости на ось OX, $t$ или $Delta t$ — интервал времени, за который произошло изменение проекции скорости.
Стоит отметить, что мы будем работать только с прямолинейным движением, поэтому нам хватит одной оси — обычно оси OX.
Для того, чтобы разобраться с использованием этого уравнения, ниже приведены примеры задач с подробными решениями и объяснениями.
Пример задачи №1 (тело разгоняется)
Подонок скатывается вниз по склону на санях с большой скоростью (см. рисунок 6). Сани прошли участок пути AB за 4 секунды. В точке A их скорость составляла
Пример задачи №2 (тело замедляется)
Смерч на санках спустился с холма и движется по горизонтальному участку CD (см. рисунок 8). На санки действует сила трения, которая замедляет их, и они останавливаются в точке D. Известно, что в точке C у санок была скорость $1.2 frac$, а участок CD был пройден ими за $6 space с$. Найдите ускорение санок на этом участке движения.
В этот раз началом отсчета времени будет момент, когда санки проходят точку C. Также проведем ось OX, параллельную участку CD (см. рисунок 9).
Тогда проекции скоростей на ось OX будут положительны и равны модулям этих векторов: при $t_0 = 0 space с$ проекция начальной скорости $upsilon_$ будет равна $1.2 frac$, а при $t = 6 space с$ проекция конечной скорости $upsilon_x$ будет равна
Упражнение №1
За указанный промежуток времени $t$ модуль скорости первого автомобиля увеличился от $upsilon_1$ до $upsilon’$, а модуль скорости второго автомобиля — от $upsilon_2$ до $upsilon’$ (на рисунке 10 изображены векторы скорости в одинаковом масштабе). Какой из автомобилей двигался в указанный промежуток с большим ускорением? Скорость какого из них возрастала быстрее?
Решение:
Давайте оценим, насколько изменились скорости автомобилей за время $t$.
Из рисунка 10 видно, что за время $t$ модуль скорости первого автомобиля увеличился на 4 единицы, в то время как модуль скорости второго автомобиля увеличился всего на 2 единицы. Поэтому первый автомобиль двигался с большим ускорением.
Так как первый автомобиль обладал большим ускорением, чем второй, то и его скорость возрастала быстрее.
Упражнение №2
Борт, наращивая скорость перед вылетом, в течение некоторого времени двигался с постоянным ускорением. Каково было ускорение самолета, если за $30 space с$ его скорость возросла с $10 frac{м}{с}$ до $55 frac{м}{с}$?
Дано: $


